算法题记录——盛最多水的容器

原题：给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。

示例：

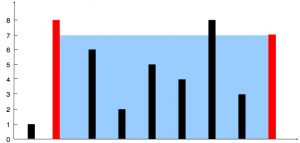
输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

思路

看到示例第一时间想到用双指针解决，关键在于何时移动左指针或右指针，并更新结果的最大值

记左指针为lp，右指针rp，记[lp, rp]区间能盛水的值为 y，由短板效应易知 *y = min(height[lp], height[rp]) (rp – lp)**

初始时令lp = 0，rp = n – 1，假设某状态下height[lp] < height[rp]，考虑此时如何移动指针

• 若将lp右移，则当 height[lp + 1] > height[lp] 时，y可能增大
• 若将rp左移，则无论 height[rp – 1] 大小，y一定减小

我们期望得到更大的值，故此时应将lp右移，反之如果height[lp] > height[rp]，则应将rp左移，然后计算新位置 y’的值与原来比较并更新最大值

代码(js)：

var maxArea = function(height) {
    let res = 0
    let lp = 0, rp = height.length - 1
    while (lp < rp) {
        if (height[lp] > height[rp]) {
            // 更新结果最大值，左移rp
            res = Math.max(res, height[rp] * (rp - lp))
            --rp
        } else {
            // 更新结果最大值，右移lp
            res = Math.max(res, height[lp] * (rp - lp))
            ++lp
        }
    }
    return res
};

再简化亿下代码：

var maxArea = function(height) {
    let res = 0
    let lp = 0, rp = height.length - 1
    while (lp < rp) {
        res = Math.max(res, height[lp] > height[rp] ? height[rp] * (rp-- - lp) : height[lp] * (rp - lp++))
    }
    return res
};

复杂度：需要遍历一遍数组，且储存双指针变量，故 时间复杂度O(n)，空间复杂度O(1)